| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 백준 줄세우기 자바
- 자바 2869
- 자바 1193
- 개발일지
- 온라인쇼핑
- 괄호의값 스택
- 인사관리사이트
- 줄세우기 위상정렬
- 백준 1193
- 백준 최소비용구하기 자바
- 백준 1806 자바
- 팀프로젝트
- 기업분석
- 웹 기술면접
- 라이브커머스
- 백준 2252 자바
- 데이터베이스 기초지식
- 1062번 가르침
- 이커머스
- 2504 괄호의값 자바
- 프로그래머스
- Union Find
- 유니온 파인드
- 백준 1700 자바
- 조인종류
- 다익스트라 최소비용구하기
- Spring Security
- 커머스기사
- 백준 괄호의값 자바
- 백준 멀티탭스케줄링 자바
Archives
- Today
- Total
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 백준 줄세우기 자바
- 자바 2869
- 자바 1193
- 개발일지
- 온라인쇼핑
- 괄호의값 스택
- 인사관리사이트
- 줄세우기 위상정렬
- 백준 1193
- 백준 최소비용구하기 자바
- 백준 1806 자바
- 팀프로젝트
- 기업분석
- 웹 기술면접
- 라이브커머스
- 백준 2252 자바
- 데이터베이스 기초지식
- 1062번 가르침
- 이커머스
- 2504 괄호의값 자바
- 프로그래머스
- Union Find
- 유니온 파인드
- 백준 1700 자바
- 조인종류
- 다익스트라 최소비용구하기
- Spring Security
- 커머스기사
- 백준 괄호의값 자바
- 백준 멀티탭스케줄링 자바
Archives
- Today
- Total
JumpUp
프로그래머스 [Lv1. 소수찾기]_ 에라토스테네스의 체 본문
수정 전 코드:
class Solution {
public int solution(int n) {
int answer = 0;
for(int i=2;i<=n;i++){
if(isPrime(i)) answer++;
}
return answer;
}
public boolean isPrime(int n){
boolean result = true; //소수이다
for(int i=2;i<=Math.sqrt(n);i++){
if(n%i==0) result = false; //소수가 아니다
}
return result;
}
}정확성 75점 효율성 0점
소수 찾기 문제에선, 에라토스테네스의 체 알고리즘을 이용해 효율적으로 소수를 찾을 수 있다.
에라토스테네스의 체란, "소수가 되는 수의 배수를 지우면 남는 건 소수가 된다"라고 생각하면 된다.
1. 2는 소수이니 체크, 2의 배수를 지워준다.
2. 3은 소수이니 체크, 3의 배수를 지워준다.
3. 5는 소수이니 체크, 5의 배수를 지워준다.
위의 과정을 계속 반복하여 남는 수는 모두 소수가 된다는 것이다.
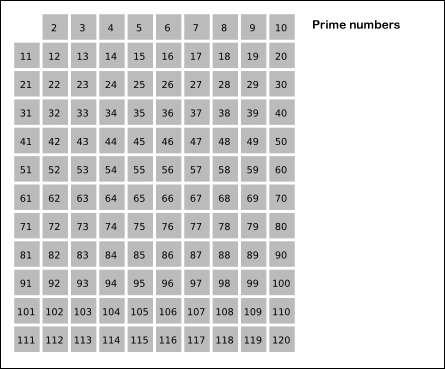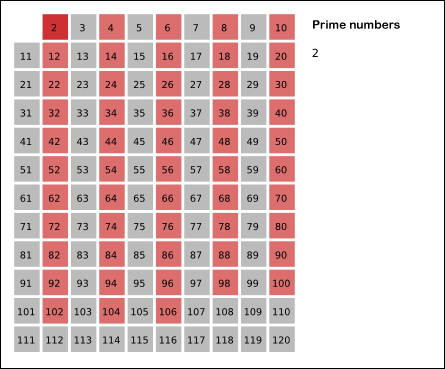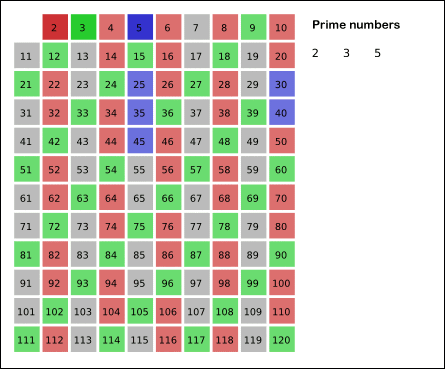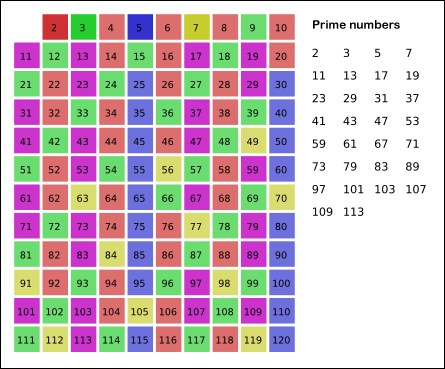
짤을 보면서 정리해보자면,
2부터 120까지의 소수를 찾는다고 했을 때,
120의 제곱근보다 작은 소수(=2,3,5,7)의 배수들을 모두 지우고 남은 수들이 소수가 된다는 것입니다.
이 알고리즘을 토대로 [소수찾기] 문제를 수정보면,
package lv1;
import java.util.ArrayList;
public class 소수찾기 {
public static void main(String[] args) {
System.out.println(solution(10));
}
public static int solution(int n){
int answer = 0;
ArrayList<Integer> primeList = new ArrayList<>(n+1);
primeList.add(0);
primeList.add(0); //0과 1은 소수 아님으로 처리
//2부터 n까지는 소수로 처리
for(int i=2;i<=n;i++){
primeList.add(1);
}
for(int i=2;i*i<=n;i++){ //n의 제곱근보다 작은 소수까지 판별
if(primeList.get(i) == 1) //소수라면,
for(int j=i*i;j<=n;j+=i) primeList.set(j,0); //소수의 배수를 지운다 (i*i 미만은 이미 처리되었으므로, j의 시작값은 i*i로 최적화할 수 있다.)
}
for(int i=0;i<=n;i++){
if(primeList.get(i) == 1) answer++;
}
return answer;
}
}
정확성과 효율성 모두 만점이 되는 것을 확인했다.
수정 전 코드와 비교해보자면,
수정 전 코드는 2부터 n까지 소수인지 아닌지 하나하나 판별하였다.
에라토스테네스의 체 알고리즘을 적용해 수정 한 코드는 n의 제곱근 보다 작은 소수까지 판별하면 되기에 훨씬 효율적이다.
728x90
'알고리즘' 카테고리의 다른 글
| 프로그래머스 [폰켓몬] (0) | 2021.04.02 |
|---|---|
| 프로그래머스 [나누어 떨어지는 숫자 배열]_Stream (0) | 2021.03.22 |
| 프로그래머스 [최대공약수와 최소공배수],[N개의최소공배수]_유클리드 호제법 gcd(a,b)=gcd(b,r) (0) | 2021.03.05 |
| [JAVA 정렬] Comparable과 Comparator (0) | 2021.02.26 |
| [JAVA] codeUp 기초100제 (0) | 2021.02.24 |




